La circularité des hauteurs
Jean-Baptiste, le 06/05/2020Traduit de l’article Pitch circularity de Diana Deutsch, professeur de psychologie à l’université de Californie à San Diego, avec l’aimable autorisation de l’auteur.
La notion de circularité
La figure ci-dessous à gauche représente un « escalier impossible », comme originellement publié par Penrose et Penrose en 19581. Dans ce modèle, chaque marche est plus basse que sa voisine immédiate dans le sens des aiguilles d’une montre, donnant l’illusion que l’escalier descend à l’infini. Notre système de perception reste bloqué sur cette interprétation, même si elle ne peut pas être correcte.
Le principe de la circularité des hauteurs est basée sur le même principe. Par analogie avec les escaliers du monde réel, les notes (ou hauteurs) sont généralement perçues comme s’étendant sur une échelle, de bas en haut, comme quand on fait glisser une main sur le clavier d’un piano. Mais elles ont aussi une dimension circulaire, le nom de la note (ou « classe de hauteur »), qui se retrouve dans notre gamme musicale, basée sur la configuration circulaire visible sur la figure ci-dessous à droite. Ainsi, en suivant cette gamme de manière ascendante par demi-tons, on parcourt les noms de note dans le sens horaire : on joue donc do, do#, ré, etc. tout autour du cercle, jusqu’à arriver à la, la# et si…et de revenir à do, do# et ré, et ainsi de suite.
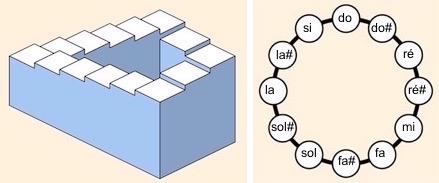
Un escalier impossible similaire à celui conçu par Penrose et Penrose (à gauche)
et une représentation du cercle des classes de hauteur (à droite)
Pour rendre compatibles ces deux dimensions, linéaire et circulaire, les théoriciens de la musique ont suggéré que les hauteurs devraient être représentées comme une hélice qui pour chaque octave effectue un tour complet sur elle-même, et où les notes séparées d’une octave se trouvent tout de même proches les unes des autres, comme ci-dessous.
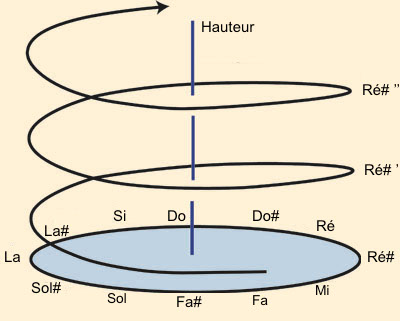
Le modèle hélicoïdal des notes
Différentes expériences
En 1964, Roger Shepard2 a imaginé qu’en créant des sons dont le nom de note est clairement défini mais dont la hauteur serait ambiguë, l’hélice pourrait s’affaisser pour former un cercle, permettant la création de gammes montant ou descendant à l’infini. Il est parvenu à créer des sons complexes, constitués seulement de composants séparés par des octaves, et dont les amplitudes étaient fixées par une enveloppe spectrale fixe en cloche. De tels sons sont clairement définis en terme de nom de note (do, ré, mi…), mais pas en terme de hauteur (à quelle octave ils sont). Quand ils sont joués de manière à parcourir dans le sens horaires le cercle des classes de hauteur, on a l’impression d’une gamme toujours ascendante : do# est entendu plus aigu que do, ré que do#, ré# que ré,……, la# que la, si, plus haut que la#, do plus haut que si, et ainsi de suite, sans fin. Dans le sens inverse des aiguilles d’une montre, on a donc l’impression d’une gamme descendant sans fin. Risset (1971)3 a créé des variantes étonnantes en utilisant des sons qui glissent et dont la hauteur semble monter ou descendre de manière continue. Pour plus de détails, voir 4.
Plus tard, j’ai imaginé qu’il devrait être possible de créer des gammes circulaires à partir de notes seules, chacune comprenant une série harmonique complète. Si vous prenez une note complexe dont vous réduisez peu à peu l’amplitude des harmoniques impaires (1, 3, 5, etc.), en gardant les harmoniques paires au même niveau, le son devrait donner l’impression de devenir plus aigu, tout en conservant le même nom de note. Dans l’exemple sonore 1, un son harmonique complexe basé sur le la 3 est présenté, avec les harmoniques impaires perdant progressivement de l’amplitude. À un moment donné, les auditeurs réalisent qu’ils écoutent la note une octave au-dessus, mais cette transition perçue est survenue sans que le son ne traverse toute la gamme ; il est resté sur la note la.
J’ai ensuite supposé que nous devrions être capables de produire des circularités de hauteurs sur le même principe. On base cette expérience sur douze sons complexes, dont les fréquences fondamentales couvrent une octave, séparés par un demi-ton. Pour le son avec la fondamentale la plus élevée, les harmoniques paires et impaires sont d’amplitudes similaires.
Puis, pour la note un demi-ton en dessous, les amplitudes des harmoniques impaires sont réduites relativement aux harmoniques paires, ce qui fait que l’on perçoit ce son plus aigu.
Puis, pour la note encore un demi-ton plus basse, les amplitudes des harmoniques impaires sont encore diminuées, le son parait encore plus aigu.
Et ainsi de suite tout au long de l’octave, par étapes d’un demi-ton, jusqu’à ce qu’on atteigne le son avec la fondamentale la plus basse. Là , les harmoniques impaires n’ont plus aucun rôle dans la perception de la hauteur du son. Le son avec la fondamentale la plus basse est donc entendu comme à l’octave supérieure, et la circularité des hauteurs est atteinte.
Voici une gamme descendante à l’infini basée sur ce principe, avec l’amplitude des harmoniques impaires réduite de 3.5 dB pour chaque baisse de demi-ton.
Et ici, une gamme ascendante basée sur le même principe :
Ici, un glissando descendant à l’infini, sur le même principe.
Ici, un glissando ascendant à l’infini, sur le même principe :
Avec mes collègues, j’ai mis au point une expérience pour déterminer si de tels sons sont effectivement entendus comme circulaires, quand tous les intervalles sont pris en compte.
Nous avons créé une banque de douze sons. Chacun de ses sons a ensuite été appairé avec les 11 autres (ex. : do-do#, do-ré, do-ré#, etc.), créant 132 paires au total.
Les sujets ont ensuite dû déterminer pour chaque paire si elle était ascendante ou descendante.
Voici un extrait de fichier audio utilisé pour cette expérience. Pour chaque paire, votre jugement correspondra probablement à la distance la plus courte entre les sons qui forment le cercle.
En appliquant le positionnement multidimensionnel aux réponses des auditeurs, on obtient des configurations à forte tendance circulaire – comme montré ci-dessous pour l’un des sujets.
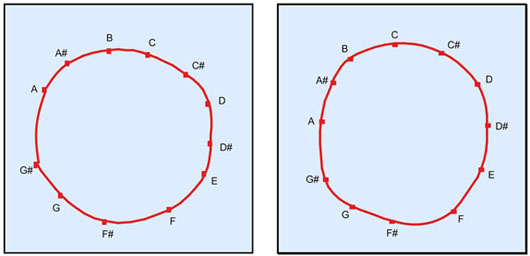
Solutions de positionnement multidimensionnel dérivées des réponses en terme de hauteur relative des sujets, basées sur les gammes circulaires de Deutsch
C’est-à -dire que la réponse du sujet ("ascendant" ou "descendant") dépend de la proximité des deux notes sur la gamme circulaire : ainsi, l’intervalle do#-ré est beaucoup plus susceptible d’être considéré ascendant, et do-si descendant. Plus les notes composant l’intervalle sont éloignées l’une de l’autre sur la gamme circulaire, plus cette tendance à répondre en fonction de leur proximité diminue.
La découverte qu’une gamme circulaire puisse être obtenue à partir de séries harmoniques complètes rend possible, de manière surprenante, l’utilisation de cet algorithme pour modifier des sons provenant d’instruments naturels de manière à ce qu’ils puissent aussi mettre en valeur la circularité des hauteurs.
William Brent, alors étudiant à l’UCSD, y est très bien parvenu en utilisant des extraits (audios) de basson, mais aussi dans une moindre mesure de hautbois, de flûte et de violon, et a montré que l’effet n’est pas détruit par le vibrato.
Cette possibilité élargit la palette de matériel musical disponible pour les compositeurs et interprètes.
Références
1. Penrose, L. S., and Penrose, R. Impossible objects: A special type of visual illusion, British Journal of Psychology, 1958, 49, 31-33. (Oscar Reutesvald a également créé un escalier impossible dans les années 1930)
2. Shepard, R. N. Circularity in judgments of relative pitch, Journal of the Acoustical Society of America, 1964, 36, 2345–2353.
3. Risset, J. C. Paradoxes de hauteur, Proceedings of the 7th International Congress on Acoustics, 1971, Budapest, S10, 613-616.
4. Deutsch, D. Paradoxes of musical pitch. Scientific American, 1992, 267, 88-95, [PDF]
5. Deutsch, D., Dooley, K., and Henthorn, T. Pitch circularity from tones comprising full harmonic series. Journal of the Acoustical Society of America, 2008, 124, 589-597. [PDF]
6. Deutsch, D. The paradox of pitch circularity. Acoustics Today, 2010, July, 8-15. [PDF]